POJ3046 Ant Counting
T种蚂蚁, 每种Ni只, 总共A只. 如果分成大小范围为S到B的集合, 能有多少种分法? {1, 2} 和 {2, 1} 是相同的两个大小为2的集合.
感觉这题和昨天做的POJ1742很像. 首先想到一个关系式:
dp[i][j][k], 表示长度为i, 集合里面元素升序排列的最后一个数字为j, 以及集合里面j的个数为k.
这样dp[i][j][k] 就可以推出 dp[i+1][j][k+1]以及 {\(dp[i+1][j+1][1…N_{j+1}]\)}
但是这样要TLE. 想办法优化, 想了好久想不出来, 感觉这样一个表已经很裸了, 而且不同的ijk组合表示不同的结构, 很难找出规律来进行化简. 看来是dp的定义错了.
换一个角度想, dp[i][j] 表示前 i 种蚂蚁组成长度为j的集合, 有多少种组合. 于是有
\[dp(i, j) = \sum_{k = 0}^{N_{i}}dp(i-1, j-k)\]
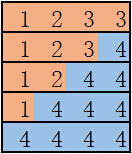
这样dp[4][j] 的诞生大概可以用下图生动的说明(假设dp[3][4] 表示有且仅有 1, 2, 3, 3 这一种情况):
#include <iostream>
#include <cstdio>
using namespace std;
inline int gint() {int n;scanf("%d", &n);return n;}
//////////////////
const int maxa = 1e5 + 10;
const int maxt = 1e3 + 10;
const int MOD = 1e6;
int T, A, S, B;
int N[maxt];
int dp[maxt][maxa];
/////////////////
void solve() { // dp[i][j] 表示前 i 种蚂蚁组成长度为j的集合, 有多少种组合.
dp[0][0] = 1;
for (int i = 1; i <= T; i++) { // 1e3
for (int j = 0; j < maxa; j++) { // 1e5
for (int k = 0; k <= N[i]; k++) if (j-k >= 0) { // 1e5
dp[i][j] = (dp[i-1][j-k] + dp[i][j]) % MOD;
}
}
}
int ans = 0;
for (int i = S; i <= B; i++) {
// printf("S = %d sum = %d\n", i, dp[T][i]);
ans = (ans + dp[T][i]) % MOD;
}
printf("%d\n", ans);
}
int main() {
scanf("%d%d%d%d", &T, &A, &S, &B);
for (int i = 0; i < A; i++) {
N[gint()]++;
}
solve();
return 0;
}
有很多重复计算, 经过艰难的修改, 加入一个 sum 数组, 剪掉了一重循环, 得到如下 MLE 代码
#include <iostream>
#include <cstdio>
using namespace std;
inline int gint() {int n;scanf("%d", &n);return n;}
//////////////////
const int maxa = 1e5 + 10;
const int maxt = 1e3 + 10;
const int MOD = 1e6;
int T, A, S, B;
int N[maxt];
int dp[maxt][maxa];
int sum[maxt][maxa];
/////////////////
void solve() { // dp[i][j] 表示前 i 种蚂蚁组成长度为j的集合, 有多少种组合.
dp[0][0] = 1;
for (int i = 1; i <= T; i++) { // 1e3
for (int j = 0; j < maxa; j++) {
sum[i-1][j] = ((j-1 < 0 ? 0 : sum[i-1][j-1]) + dp[i-1][j]) % MOD;
}
for (int j = 0; j < maxa; j++) { // 1e5
int total = sum[i-1][j];
if (j - N[i] - 1 >= 0)
total -= sum[i-1][j-N[i]-1];
dp[i][j] = (dp[i][j] + total) % MOD;
}
}
int ans = 0;
for (int i = S; i <= B; i++) {
ans = (ans + dp[T][i]) % MOD;
}
printf("%d\n", ans);
}
int main() {
scanf("%d%d%d%d", &T, &A, &S, &B);
for (int i = 0; i < A; i++) {
N[gint()]++;
}
solve();
return 0;
}
最后用上滚动数组, 并加入up变量, 得到以下 AC 代码:
#include <iostream>
#include <cstdio>
#include <cstring>
using namespace std;
inline int gint() {int n;scanf("%d", &n);return n;}
//////////////////
const int maxa = 1e5 + 10;
const int maxt = 1e3 + 10;
const int MOD = 1e6;
int T, A, S, B;
int N[maxt];
int dp[2][maxa];
int sum[2][maxa];
/////////////////
void solve() { // dp[i&1][j] 表示前 i 种蚂蚁组成长度为j的集合, 有多少种组合.
dp[0][0] = 1;
int up = 0;
for (int i = 1; i <= T; i++) { // 1e3
up += N[i];
for (int j = 0; j <= up; j++) {
sum[(i-1)&1][j] = ((j-1 < 0 ? 0 : sum[(i-1)&1][j-1]) + dp[(i-1)&1][j]) % MOD;
}
for (int j = 0; j <= up; j++) { // 1e5
int total = sum[(i-1)&1][j];
if (j - N[i] - 1 >= 0)
total -= sum[(i-1)&1][j-N[i]-1];
dp[i&1][j] = (total) % MOD;
}
}
int ans = 0;
for (int i = S; i <= B; i++) {
ans = (ans + dp[T&1][i]) % MOD;
}
printf("%d\n", ans);
}
int main() {
scanf("%d%d%d%d", &T, &A, &S, &B);
for (int i = 0; i < A; i++) {
N[gint()]++;
}
solve();
return 0;
}
这道题做完, 感觉我对 dp 还是非常的不熟悉, 不知道判断一个思路方向是否是死胡同, 转换角度不够快; 由于对细节的追求不够严谨, 导致优化的时候要额外考虑很多边界问题. 尤其是最后一个 up 变量的添加, 想了好久- -!